Abstract
abstract
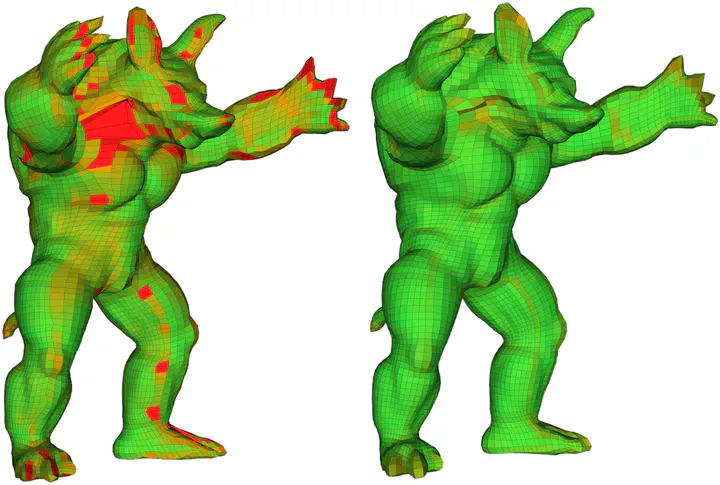
AbstractThe usability of hexahedral meshes depends on the degree to which the shape of their elements deviates from a perfect cube; a single concave, or inverted element makes a mesh unusable. While a range of methods exist for discretizing 3D objects with an initial topologically suitable hex mesh, their output meshes frequently contain poorly shaped and even inverted elements, requiring a further quality optimization step. We introduce a novel framework for optimizing hex-mesh quality capable of generating inversion-free high-quality meshes from such poor initial inputs. We recast hex quality improvement as an optimization of the shape of overlapping cones, or unions, of tetrahedra surrounding every directed edge in the hex mesh, and show the two to be equivalent. We then formulate cone shape optimization as a sequence of convex quadratic optimization problems, where hex convexity is encoded via simple linear inequality constraints. As this solution space may be empty, we therefore present an alternate formulation which allows the solver to proceed even when constraints cannot be satisfied exactly. We iteratively improve mesh element quality by solving at each step a set of local, per-cone, convex constrained optimization problems, followed by a global energy minimization step which reconciles these local solutions. This latter method provides no theoretical guarantees on the solution but produces inversion-free, high quality meshes in practice. We demonstrate the robustness of our framework by optimizing numerous poor quality input meshes generated using a variety of initial meshing methods and producing high-quality inversion-free meshes in each case. We further validate our algorithm by comparing it against previous work, and demonstrate a significant improvement in both worst and average element quality.
[ project page ] [ Video ]